Everything Is Fast For Small n
Let’s say you’re about to deploy an application. Said app has been heavily tested by your development team, who have all been infected by unit testing fever. It’s also been vetted by your QA group, who spent months spelunking into every crevice of the app. You even had a beta test period with real live users, who dutifully filed bugs and put the application through its paces before finally signing off on the thing.
Your application is useful and popular. Your users love it. Your users love you. But over the next week, something curious happens. As people use the application, it gets progressively slower and slower. Soon, the complaints start filtering in. Within a few weeks, the app is well-neigh unusable due to all the insufferable delays it subjects users to – and your users turn on you.
Raise your hand if this has ever happened to a project you’ve worked on. If I had a buck for every time I’ve personally seen this, I’d have enough for a nice lunch date. Developers test with tiny toy data sets, assume all is well, and then find out the hard way that everything is fast for small n.
I remember a client-side Javascript sort routine we implemented in a rich intranet web app circa 2002. It worked great on our small test datasets, but when we deployed it to production, we were astonished to find that sorting a measly hundred items could take upwards of 5 seconds on a user’s desktop machine. JavaScript isn’t known for its speed, but what the heck?
Well, guess which sort algorithm we used?

InsertSort is n2 (worst case), ShellSort is n3/2, and QuickSort is n log n. But we could have done worse – we could have picked Bubble Sort, which is n2 even in the best case.
Friends, do not do this. Test your applications with large data sets, at least large enough to cover your most optimistic usage projections over the next year. Otherwise, you may be sorry. And your users definitely will be sorry.
Big O notation is one of those things that’s easier seen than explained. But it’s a fundamental building block of computer science.
Big O notation: A theoretical measure of the execution of an algorithm, usually the time or memory needed, given the problem size n, which is usually the number of items. Informally, saying some equation f(n) = O(g(n)) means it is less than some constant multiple of g(n). The notation is read, “f of n is big oh of g of n.”
Developers rely on data structures and databases that have favorable big O notation performance baked in, without thinking much about it. But if you stray from those well-worn paths, you can be in a world of performance pain – and much sooner than you could have possibly imagined. The importance of big O notation is best illustrated in this graph from Programming Pearls:
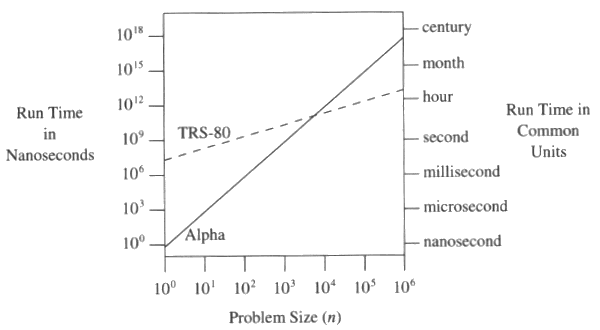
The TRS-80 algorithm is 48n, and the DEC Alpha algorithm is n3.
When n is 10, they’re within a second of each other. But when n grows to 100,000, the modern DEC Alpha takes a month to do what a prehistoric TRS-80 can accomplish in a few hours. Having a big O notation bottleneck in your app is a one-way ticket in the performance Wayback Machine to 1997 – or worse. Much worse.
There are friendly names for the common big O notations; saying “n squared” is equivalent to saying “quadratic:”
| notation | friendly name |
| O(1) | constant |
| O(log n) | logarithmic |
| O([log n]c) | polylogarithmic |
| O(n) | linear |
| O(n log n) | sometimes called "linearithmic" or “supralinear” |
| O(n2) | quadratic |
| O(nc) | polynomial, sometimes "geometric" |
| O(cn) | exponential |
| O(n!) | factorial |
Tom Niemann has handy charts that compare the growth rates of common algorithms, which I’ve adapted here:
| n | lg n | n7/6 | n lg n | n2 | 7/6n | n! |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 16 | 4 | 25 | 64 | 256 | 12 | 20.9 trillion |
| 256 | 8 | 645 | 2,048 | 65,536 | 137 quadrillion | - |
| 4,096 | 12 | 16,384 | 49,152 | 16,777,216 | - | - |
| 65,536 | 16 | 416,128 | 1,048,565 | 4,294,967,296 | - | - |
| 1,048,476 | 20 | 10,567,808 | 20,969,520 | 1.09 trillion | - | - |
| 16,775,616 | 24 | 268,405,589 | 402,614,784 | 281.4 trillion | - | - |
Here are sample execution times, assuming one unit of execution is equal to one millisecond of CPU time. That’s probably far too much on today’s CPUs, but you get the idea:
| n | lg n | n7/6 | n lg n | n2 | 7/6n | n! |
| 1 | <1 sec | <1 sec | <1 sec | <1 sec | <1 sec | <1 sec |
| 16 | <1 sec | <1 sec | <1 sec | <1 sec | <1 sec | 663 years |
| 256 | <1 sec | <1 sec | 2 sec | 65 sec | 4.3 mlln yrs | - |
| 4,096 | <1 sec | 16 sec | 49 sec | 4.6 hr | - | - |
| 65,536 | <1 sec | 7 min | 17 min | 50 days | - | - |
| 1,048,476 | <1 sec | 3 hr | 6 hr | 35 years | - | - |
| 16,775,616 | <1 sec | 3 days | 4.6 days | 8,923 years | - | - |
Notice how quickly we get into trouble as the number of items (n) increases. Unless you’ve chosen data structures that offer ideal near-logarithmic performance across the board, by the time you get to 4,096 items you’re talking about some serious CPU time. Beyond that, I used dash as shorthand for “forever.” That’s how bad it can get.
Everything is fast for small n. Don’t fall into this trap. It’s an easy enough mistake to make. Modern apps are incredibly complex, with dozens of dependencies. Neglect to index one little field in your database and you’re suddenly back in TRS-80 land. The only way to truly know if you’ve accidentally slipped an algorithmic big O bottleneck into your app somewhere is to test it with a reasonably large volume of data.