Attending yesterday's Halo 3 launch event at the Silicon Valley Microsoft campus -- and the large Halo3 tournament we helped moderate -- got me thinking about player ranking and matching systems. Without a well-designed ranking and matching system in place, you'll get horribly mismatched games, where one team demolishes the other by a margin of 3x or more. This is counterproductive for both teams:

• The higher skilled team learns absolutely nothing by defeating their underskilled opponent. They're coasting by without a challenge. I suppose it's fun, in a way, to win every match and crush your opponents. But it's ultimately an empty and meaningless style of play.

• The lower skilled team is demoralized by a total, crushing defeat at the hands of the higher skilled team. There's no incentive to continue. And when you're consistently matched against opponents that you have no chance of winning against, why play at all?

An ideal system would always match players of approximately equal skill against each other. How do you know when you've achieved that goal? You look at the data. The record of wins, losses, and ties for each player provides the answer: if the matching and ranking system is working properly, every player or team will eventually plateau at a skill level where they are winning about 50% of the time.

There are dozens of possible ranking and rating systems we could use. Christopher Allen and Shannon Appelcline's post Collective Choice: Competitive Ranking Systems explores many of them. But perhaps the most famous ranking system is the Elo rating system, which originated in the chess world. It's a simple statistical model used to objectively rate player skill levels:

Here's how Elo works:

• A new player is assigned a default rating, say 1200.
• Two players compete, with one of three results: win, loss, tie.
• The two player's ratings are fed into an algorithm along with the end state of the game. A new rating for each player is returned.

Let's say two players, both rated 1200, play a game. Player 1 wins. Player 1 will now be rated 1205 and player 2 will be rated 1195.

Players that win a lot will achieve higher ratings. But the higher rated player also starts to see diminishing returns for defeating low ranked players. In order to increase his rank, he must defeat other higher ranked players. If a high ranked player loses to a low ranked player, he loses much more of his rating then he'd gain if he won the match.

Over time the game players will end up being rated based on their Elo skill level rather than other factors.

It's simpler than it seems. Let me put this in language us geeks can understand: you gain more XP from slaying a massive, mighty dragon than you do from beating up on a common wharf rat.

As you level up, it's entirely possible that you may become so very powerful that you'll have to move on from those massive dragons to even more intimidating opponents. Seems obvious enough to those of us who understand the statistical conventions of Dungeons and Dragons.

The Elo system, like the Dungeons and Dragons system, is proven to work. Although it was originally designed to rank chess players, it's used throughout the online and offline gaming worlds to rank and match players, in everything from Pokemon to Scrabble to World of Warcraft.

When it comes to matching players online, Blizzard Entertainment is arguably one of the most experienced companies on the planet. They pioneered online ranking systems back in 1996 with Diablo and battle.net, and extended that lead through Starcraft, Diablo II, Warcraft III, and the juggernaut that is World of Warcraft. Blizzard has collectively matched and ranked millions of players-- if anyone knows how to get this right, it's Blizzard.

Warcraft III is an excellent case study in player ranking and matching. Despite Blizzard's prior experience, and even though it uses the proven Elo ranking system, Warcraft III had a lot of problems matching players -- problems that took years for Blizzard to work out. I myself was an avid Warcraft III ranked player for about a year, so I've experienced this first hand. Warcraft III's automatic matching system was radically overhauled with Patch 1.15 in 2004, a full two years after the game was released. If you scrutinize the Blizzard support FAQs, you can read between the lines to see where the exploits and pathologies are:

1. Until a player has played a certain number of games, their performance will be highly variable, and accurately matching them is difficult.

The skill of players with low-level accounts can vary radically, from a player who has just begun playing multiplayer games of Warcraft III to a highly experienced player who has played hundreds of games but has just created a new account. Novice players would all too often find themselves in unfair matches against very skilled opponents. In an attempt to better match players of similar skill together into games, Battle.net's matchmaking system no longer uses a player's level as the only determining factor when creating games.

2. Unless players are consistently playing games, their rating should decay over time.

Players may lose XP if they do not play a minimum number of games per week, as listed on Chart 1. Failure to play the minimum game requirement during a week results in an XP penalty. For each game you don't play below the amount required for your level, you incur one loss [to an opponent of the same skill level].

3. Players cannot cherry-pick opponents or environments to improve their ranking. They must play randomly chosen opponents on neutral ground.

Battle.net's ladder system has been revamped for Warcraft III. This new system promotes active competition and maintains the ladder's integrity. The anonymous matchmaking system (AMM) prevents win trading and ensures that high-level players face opponents of similar skill. The AMM anonymously matches players based on skill level, and randomly selects maps based on the players' preferences. Players can choose their race, but most other game options are preset by the designers, resulting in a higher level of play.

If you're not into anonymous play, arranged team games are possible, but they are isolated on a special ladder of their own. This is done to prevent any kind of player collusion from tainting the main ladder results.

You can find many of the very same dangers echoed in the "practical issues" section of the Elo rating Wikipedia entry. Chess games and real-time strategy games are completely different things, but they have strikingly similar ranking and matching pathologies.

One particular weakness of the Elo system is the overly simplified assumption that the performance of every player will follow a normal distribution. This is a more severe problem than you might think, as it disproportionately affects new and beginning players. As Blizzard noted above, "Novice players would all too often find themselves in unfair matches against very skilled opponents." For many games, a large proportion of your audience will be novices. If these novice players experience several bad mismatches, they may never come back, and pretty soon you won't have a community of gamers to match anyone against.

Most modern implementations of the Elo system make adjustments to rectify this glaring flaw:

Subsequent statistical tests have shown that chess performance is almost certainly not normally distributed. Weaker players have significantly greater winning chances than Elo's model predicts. Therefore, both the USCF and FIDE have switched to formulas based on the logistic distribution. However, in deference to Elo's contribution, both organizations are still commonly said to use "the Elo system".

Perhaps the most modern variant of Elo is Microsoft's TrueSkill ranking system used on its Xbox Live online gaming network. The TrueSkill system has better provisions for scoring team games, whereas Elo is based on the single player per game model. But TrueSkill's main innovation is incorporating the uncertainty of a player's rating deeply into the mathematical model.

Rather than assuming a single fixed skill for each player, the system characterises its belief using a bell-curve belief distribution (also referred to as Gaussian) which is uniquely described by its mean μ (mu) ("peak point") and standard deviation σ (sigma) ("spread"). An exemplary belief is shown in the figure.

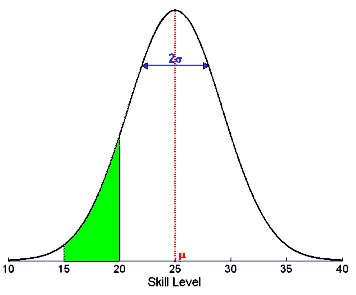
Note that the area under the skill belief distribution curve within a certain range corresponds to the belief that the player's skill will lie in that range. For example, the green area in the figure on the right is the belief that the player's skill is within level 15 and 20. As the system learns more about a player's skill, σ has the tendency to become smaller, more tightly bracketing that player's skill. Another way of thinking about the μ and σ values is to consider them as the "average player skill belief" and the "uncertainty" associated with that assessment of their skill.

It's more complex math than the relatively simple classic Elo ranking system, but TrueSkill should result in more accurate ranking and matching. Remember, that's why we're doing this: to achieve the best possible gameplay experience for all players, not just the elite players who have hundreds of games under their belt.

Our goal is to match players of all skill levels to their counterparts, and to let players reliably rise in rank until they reach a natural plateau of 50% win/loss ratio. We don't want blowouts. We want nail-biting, edge-of-your-seat cliffhangers every time, games that go down to the wire. We will know we've succeeded when each player feels like every game was the equivalent of slaying a massive, mighty dragon-- and not beating up on some puny wharf rats.